What Is Sierpinski S Carpet

It s a good practice to use virtualenvs to isolate package requirements.

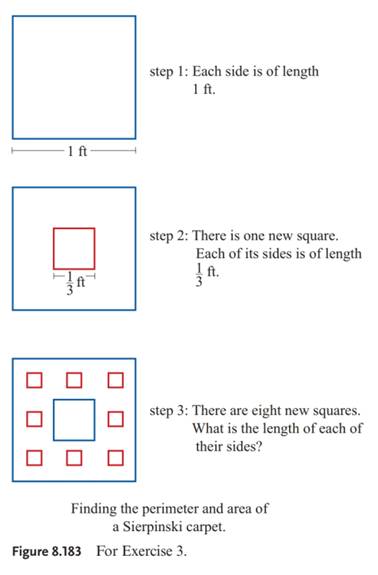
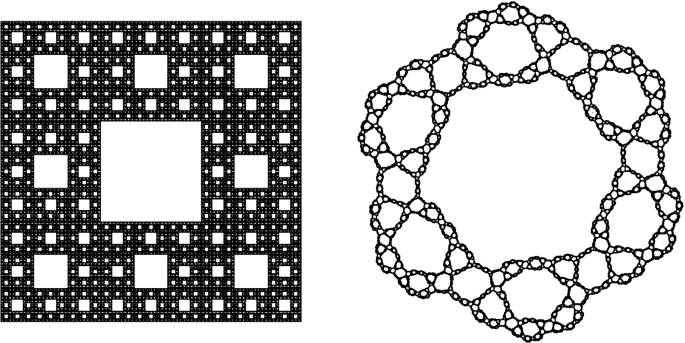
What is sierpinski s carpet. For instance subdividing an equilateral triangle. The carpet is one generalization of the cantor set to two dimensions. The squares in red denote some of the smaller congruent squares used in the construction. Creating one is an iterative procedure.

Remove the middle one. Here are 6 generations of the fractal. Explore number patterns in sequences and geometric properties of fractals. The sierpinski triangle i coded here.

What is the area of the figure now. Here s the wikipedia article if you d like to know more about sierpinski carpet. The sierpinsky carpet is a self similar plane fractal structure. This is a fun little script was created as a solution to a problem on the dailyprogrammer subreddit community.

You keep doing it as many times as you want. The sierpiński carpet is the fractal illustrated above which may be constructed analogously to the sierpiński sieve but using squares instead of triangles it can be constructed using string rewriting beginning with a cell 1 and iterating the rules. The sierpinski carpet is the intersection of all the sets in this sequence that is the set of points that remain after this construction is repeated infinitely often. Remove the middle one from each group of 9.

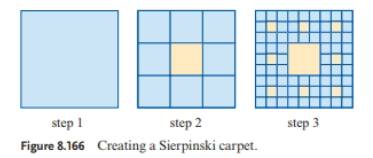
The area of sierpinski s carpet is actually zero. Divide each one into 9 equal squares. Originally constructed as a curve this is one of the basic examples of self similar sets that is it is a mathematically generated. Step through the generation of sierpinski s carpet a fractal made from subdividing a square into nine smaller squares and cutting the middle one out.

This tool lets you set how many cuts to make number of iterations and also set the carpet s width and height. Divide it into 9 equal sized squares. To construct it you cut it into 9 equal sized smaller squares and remove the central smaller square from all squares. The technique of subdividing a shape into smaller copies of itself removing one or more copies and continuing recursively can be extended to other shapes.

The sierpiński triangle sometimes spelled sierpinski also called the sierpiński gasket or sierpiński sieve is a fractal attractive fixed set with the overall shape of an equilateral triangle subdivided recursively into smaller equilateral triangles. Another is the cantor dust. Sierpinski s carpet also has another very famous relative. The sierpiński carpet is a plane fractal first described by wacław sierpiński in 1916.

The figures below show the first four iterations. Take the remaining 8 squares. How to construct it.